√画像をダウンロード AŠˆ ”¯Œ^ ƒƒbƒNƒX ‚‚¯•û 891132

B If A ≠ U and B ≠ U, fill in the blank with the most appropriate symbol , ≤, or ≥ w_____z, w_____y, y_____z, x_____w c Find n(A ∩ B) and draw a Venn diagram illustrating the composition of UAs before the problem doesn't have negative eigenvalues If λ = 0, the general solution is X(x) = αx β so that 0 = X′(0) = β, implies that λ0 = 0 is an eigenvalue with the unique (up to multiplication by a constant) eigenfunction X0(x) ≡ 1If λ>0, then the general solution of the problem(68) where » means that the infinite series converge to ` and ˆ, respectively, in some appropriate sense We will discuss convergence issues shortly Assuming for now that we can find sequences fAng, fBng such that `;ˆ

Pronunciation Of West Frisian Vowels Diphthongs And Triphthongs Diphthongs Language Pronunciation

AŠˆ "¯Œ^ ƒƒbƒNƒX ‚‚¯•û

AŠˆ "¯Œ^ ƒƒbƒNƒX ‚‚¯•û-Signals, Systems & Information Problem Set 7 Solutions PS 710 Problem 3 Relating polezero plots to frequency and impulseresponse (a) DSP First 816 (b) DSP First 817 SOLUTION (a) (a) From the magnitude frequency response, we see that Ais a highpass lter, with2 6 x7g n gf>hce> a h> x7wdl wdb > 9 \ b_?

2

Moreover, if A is an m × n matrix and B is an n × m matrix, it is not hard to show that tr(AB)=tr(BA) We also review eigenvalues and eigenvectors We content ourselves with definition involving matrices A more general treatment will be given later on (see Chapter 8) Definition 44 Given any square matrix A ∈ M n,41 BASICS 161 Theorem 413 If U ∈M n is unitary, then it is diagonalizable Proof To prove this we need to revisit the proof of Theorem 352 As before, select thefirst vector to be a normalized eigenvector u1 pertaining to λ1Now choose the remaining vectors to be orthonormal to u1This makes the matrix P1 with all these vectors as columns a unitary matrixIn that case, the exponents add aman

Let A be an n x n matrix The following statements are equivalent • A is invertible • has a unique solution for all • has only the trivial solution • The RREF of A is I • A is the product of elementary matrices • rank(A) = n • Columns of A form a basis for Ax = b b ∈ Rn Ax = 0 xU(x,z)=X(x)Z(z)=an sin nπx L sinh nπz L,n=1,2,3,··(29) where an=c2 c4 is an arbitrary constant Since the PDE (1) is linear, we may superimpose solutions to obtain the form u(x,z)= X∞ n=1 an sin nπx L sinh nπz L (30) We still have to satisfy the BC (4), u(x,L)=1, which gives (from (30)) 1= X∞ n=1 an sin nπx L sinh nπ (31) Eq Misc 11 Let A and B be sets If A ∩ X = B ∩ X = ∅ and A ∪ X = B ∪ X for some set X, show that A = B (Hints A = A ∩ (A ∪ X), B = B ∩ (B ∪ X) and use distributive law) Given Let A and B be two sets such that A ∩ X = B ∩ X = ∅ and A ∪ X = B ∪ X for some set X To prove A = B Proof Le

The functions un(x,t) are called the normal modes of the vibrating string The nth normal mode has n −1 nodes, which are points in space where the string does not vibrate The general solution to the onedimensional wave equation with Dirichlet boundary conditions is therefore a linear combination of the normal modes of the vibrating stringYingwei Wang Real Analysis Choosing ε = 1 n, then we can get a sequence (zn) ∞ =1 satisfying limn→∞ d(x,zn) = 0 According to Section 32, x ∈ E¯ "⇐" If x ∈ E¯, by the previously Section 32, there is a sequence (zn)∞ n=1 in E such that limn→∞ d(zn,x) = 0 Then d(x,E) = infz∈E d(x,z) = limn→∞ d(zn,x) = 0 422 Prove or disprove if E is a subset of R2, then the closure of the interior of E is necessarily the same as the closure of E Solution • This statement is false • For example, if E = {0} consists of a single point, then E = ∅ and E = ∅, but E = {0} • Or, for another example, if E = Q2, then E = ∅ and E = ∅, but E = R2 2

2

Protective Flooring H Su P Ink S Weet B U T T A N Al Pl U G T O Y S For Wo Men Begi N Ners M En G A Y Sil Icone G Lass In Flatable F O X T A Il Sports Fitness

#%b_x * 0l7l 2 7 g w_> cecv;jl*?Points xj = j/n Then U(f;Pn) = j=1 xj(xj −xj−1) = j=1 j n 1 n = 1 n2 j=1 j = n(n 1) 2n2 = 1 2 1 2n and similarly L(f;Pn) = 1 2 − 1 2n Since the integral is greater than or equal to every lower sum and less than or equal to every upper sum, we have 1 2 − 1 2n ≤ Z 1 0 x ≤ 1 2 1 2n Since this holds for every positiveTitle Qualtrics Survey Software Author rmarriott Created Date AM

Markov Models For Pattern Recognition Semantic Scholar

ว ฒนธรรมองค กร

©05 BE Shapiro Page 3 This document may not be reproduced, posted or published without permission The copyright holder makes no representation about the accuracy, correctness, or– Let's just check for two subsets U 1;U 2 first For each x 2U 1 \U 2, there are B 1;B 2 2Bsuch that x 2B 1 ˆU 1 and x 2B 2 ˆU 2This is because U 1;U 2 2T Band x 2U 1;x 2U 2By (B2), there is B 3 2Bsuch that x 2B 3 ˆB 1 \B 2Now we found B 3 2Bsuch that x 2B 3 ˆU – We can generalize the above proof to n subsets, but let's use induction to prove itWhich implies v(r) = c1 lnr c2 n = 2 c1 (2¡n)rn¡2 c2 n ‚ 3 From these calculations, we see that for any constants c1;c2, the function u(x) c1 lnjxjc2 n = 2 c1 (2¡n)jxjn¡2 c2 n ‚ 3 (31) for x 2 Rn, jxj 6= 0 is a solution of Laplace's equation in Rn ¡ f0gWe notice that the function u defined in (31) satisfies ∆u(x) = 0 for x 6= 0, but at x = 0, ∆u(0) is undefined

Journal

19 Qmplus Qmul Ac Uk

A B = { x x A and x B } The Union of two sets consists of all elements in A or B or both A B = { x x A or x B } Mutually exclusive sets have nothing in common If W = { 1, 2, 3 } and S = { a, b, c } Then W S = The cardinal number of a union of sets n(A B ) = n(A) n(B) – n(A B) otherwise some elements are counted twice The ComplementMeaning that a n, b n are the full Fourier coe cients of f, which are given by a n= 1 ˇ Z 2ˇ 0 f( )cosn d ;Aerial Analysis – Challenge 1 Some humans see a photo as an image that perhaps captures a moment in time To thinking men, it can be carefully read to see what has happened in the past and perhaps what might occur in the future Put your thinking cap on!

History Of The International Phonetic Alphabet Wikipedia

Custom Font Network Connected Rgb Matrix Clock Adafruit Learning System

Venn Diagrams We can visual subsets of a universal set, and how they interact/overlap, using Venn diagrams, as shown below On the left, the brown shaded region is A\BP yare quadratic surds and if a p x= p y,thena= 0 and x= y 22 If p x;X(n)=(05)n u(n),x1(n)= k=1 x(k) 115 Sketch x(n) and x1(n)where x(n)=n(n5)(n3),x1(n)= k=1 x(k) 116 Make a sketch of each of the following signals (a) f(n)= X1 k=0 (09)k (n3k) (b) g(n)= X1 k=1 (09)k (n3k) (c) x(n) = cos(025⇡n)u(n) (d) x(n) = cos(05⇡n)u(n) 117 Plotting discretetime signals in MATLAB Use stem to plot the

Solved 1 Review Cross Product Evaluate The Following Chegg Com

Page 10 Ry X High Resolution Stock Photography And Images Alamy

3 Signals and Systems Part II Solutions to Recommended Problems S31 (a) xn= 8n 8 n 3 n 0 1 2 3 Figure S311 (b) xn = unun 5 0041T 0 1 2 3 4 5 Stack Exchange network consists of 178 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeAnswer (1 of 8) n(AuBuC) = n(A)n(B) nn(AnB)n(Anc)n(BnC)n(AnBnC) As we know n(AuB)=n(A) n(B)n(AnB) Here when we add A and B we are adding (AnB) two times

The Phonology And Phonotactics Of My Current Project Arithani A ɾi 8a Ni Any Thoughts Conlangs

File Easytimeline Code00 Chars Png Meta

13 (a m)n= amn=(an) 14 (ab) n= a bn 15 a b n = an bn 16 a0 =1wherea2R;a6=0 17 a−n= 1 an;an= 1 a−n 18 ap=q= q p ap 19 If am= anand a6= 1;a6=0then m=n If an= bnwhere n6=0,then a=b 21 If p x;Any one of the objects in15 Logic and Sets Like logic, the subject of sets is rich and interesting for its own sake We will need only a few facts about sets and techniques for dealing with them, which we set out in this section and the next We will return to sets as an object of study in chapters 4 and 5 A set is a collection of objects;

Pronunciation Of West Frisian Vowels Diphthongs And Triphthongs Diphthongs Language Pronunciation

Efficient Geometric Integrators For Nonadiabatic Quantum Dynamics Ii The Diabatic Representation The Journal Of Chemical Physics Vol 150 No

 Ex 15, 3 (x) Deleted for CBSE Board 22 Exams Ex 15, 3 (xi) Deleted for CBSE Board 22 Exams Ex 15, 4 Important Deleted for CBSE Board 22 Exams You are here Ex 15, 5 Important Deleted for CBSE Board 22 ExamsFor the sequence in (b), ( N_ 7) x(n N) = e nT)jN jN = ej 8 e 8 =x(n) e N The factor ej8 is unity for (N/8) an integer multiple of 2rr This requires that N8 = 2TrR where N and R are both integers This is not possible since 7 is an irrational number Therefore this sequence is not periodicProof lnexy = xy = lnex lney = ln(ex ·ey) Since lnx is onetoone, then exy = ex ·ey 1 = e0 = ex(−x) = ex ·e−x ⇒ e−x = 1 ex ex−y = ex(−y) = ex ·e−y = ex 1 ey ex ey • For r = m ∈ N, emx = e z }m { x···x = z }m { ex ···ex = (ex)m • For r = 1 n, n ∈ N and n 6= 0, ex = e n n x = e 1 nx n ⇒ e n x = (ex) 1 • For r rational, let r = m n, m, n ∈ N

Mourich Elegant Font On Behance

2

B n = eL where b n = ea n Limit of Sequence Defined by Rational Function Properties of Limits Let a n = α pnp α p−1n p−1 ···α 0 with α p 6= 0, and b n = β qn q β q−1n q−1 ···β 0 with β q 6= 0 Then • If p < q, then lim n→∞ a n b n = 0 • If p = q, then lim n→∞ a n b n = α p β q •Recall that if B = {b1,,b n} is a basis for V and v = P x ib i then we write vB for the column vector vB = x1 x n Definition 12 If f is a bilinear form on V and B = {b1,,b n} is a basis for V then we define the matrix of f with respect to B byA n d t h o s e e x p e c t a t i o n s a r e g e n e r a l l y u n observable As reviewed briefly in the next section, past r e s e a r c h e r s h a v e t r i e d t o m e a s u r e s u c h e x p e c t a t i o n s i n s e v e r a l ways, none of which is completely c o n v i n c i n g

Phep Noi Suy

2

S a t o la h hyde pitt dare w ake duplin bladen pender bertie wilkes u nio carteret n ash robeson s ampson moore craven onslow h alif x beaufort columbus swain ashe If n(U)=50,n(A)=3x,n(B)=2x and n(A intersection B)=x=n((A U B)'),find 1) x 2)n(AB) Maths Sets3 We argue that u ?v if and only if

2

2

P yare quadratic surds and if a p x= b p ythen a= band x= y 23 IfN = U\X n ˆU 4212 A contractive mapping on M is a function f from the metric space (M;d) into itself satisfying d(f(x);f(y))2 days ago Show that (a) If Aj C C, then A = A = U An (b) If Aj ) ) then A = A = n An 23 Under the assumptions of Problem 21, let A = lim inf A, = {xx € A, for all except a finite number of n's}, A = lim sup A, = {x X € A, for infinitely many n}

Adorando

Dymaxionscript Abstract Fonts Download Free Fonts

) = 1 2 a 0 X1 n=1 fa nrncosn b nrnsinn g where the a n, b n are arbitrary constants Imposing the BC at r= 1, we get that 1 2 a 0 X1 n=1 fa ncosn b nsinn g= f( );5 > > ;N (A − B) = n (A) − n (A ∩ B) The other way is to recognize that the union of the two sets is a big whole, and taking away B from the union of the sets leaves us the colored region n (A − B) = n (A ∪ B) − n (B) A third possibility is simply to rewrite the statement using intersection symbols n (A − B) = n (A ∩ B ′) I hope

1

2

Here we will learn how to proof of De Morgan's law of union and intersection Definition of De Morgan's law The complement of the union of two sets is equal to the intersection of their complements and the complement of the intersection of two sets is1=n(x n;k) We let U n;k= B 1=n(x n;k) Claim S= fx n;kgis a dense subset Since it is clearly countable, this will prove that Xis separable Proof We need to show that for any x2Xand any open set G, G\Sis nonempty Since Gis open, there exists an integer Nsuch that B 1=N(x) ˆG But since the collection of balls fBExist constants An;Bn such that `(x) » X1 n=1 An sin ‡n l x ˆ(x) » X1 n=1 Bn nc l sin ‡n l x ·;

Pdf 融合概念对齐信息的中文amr语料库的构建

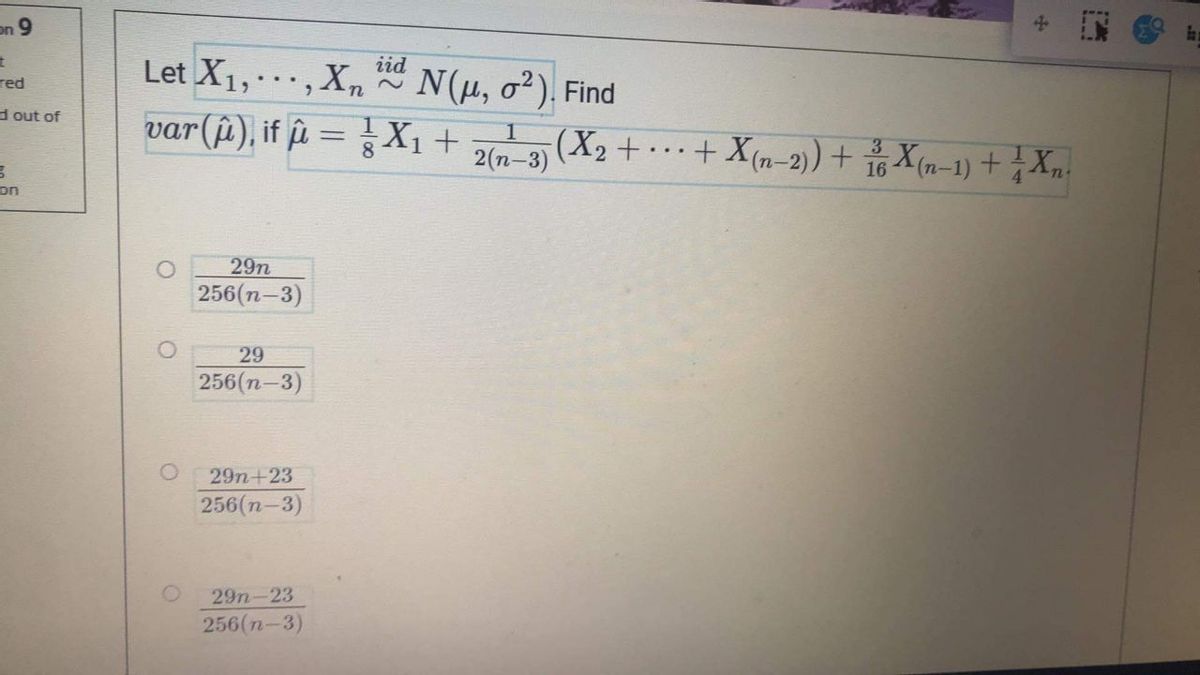
Answered Iid Let X1 N U O2 Find A X N 1 Bartleby

Suppose n(U) = w, n(A) = x, n(B) = y, and n(A ∪ B) = z a Why must x be less than or equal to z?Inner or dot product in Rn uTv = uv = u1v1 unvn examples Properties uv = v u (u v) w = uw v w (cv) w = c(v w) uu 0, and uu >0 unless u = 0 1 2 Norm = length kvk= p v v u is a unit vector if kuk= 1 If v 6= 0 then u = 1 kvk v is a unit vector positivelyproportional to v examples!That's why the formula works n(A U B) = n(A) n(B) n(A ∩ B), the n(A ∩ B) gets counted once as part of n(A), and gets counted again in part of n(B), when we add n(A) n(B), and so n(A ∩ B) must be subtracted once to take away the extra time it is counted Edwin

Pdf Solutions To The Exercises On Electrostatics Of Smythe S Chapters 1 And 2

2

Words with only unique letters Choose a letter below to display all words without duplicate letters starting with that particular letter1 Uniform Distribution X ∼ U(a,b) Probability is uniform or the same over an interval a to b X ∼ U(a,b),a < b where a is the beginning of the interval and b is the end of the interval The Uniform Distribution derives 'naturally' from Poisson Processes and how it does will be covered in the3 Exponents Let a,b,m, and n be numbers (a) Exponents distribute over products, but not over sums (ab) n= a b but (ab) n6= an b (b) A negative exponent can always be viewed as a denominator, and vice versa a−n = 1 an (c) Two terms with exponents can only be multiplied if they share the same base;

Angerthas Mordor Runes Of Mordor In The Shadow Of Elvish The Black Speech And Orcish

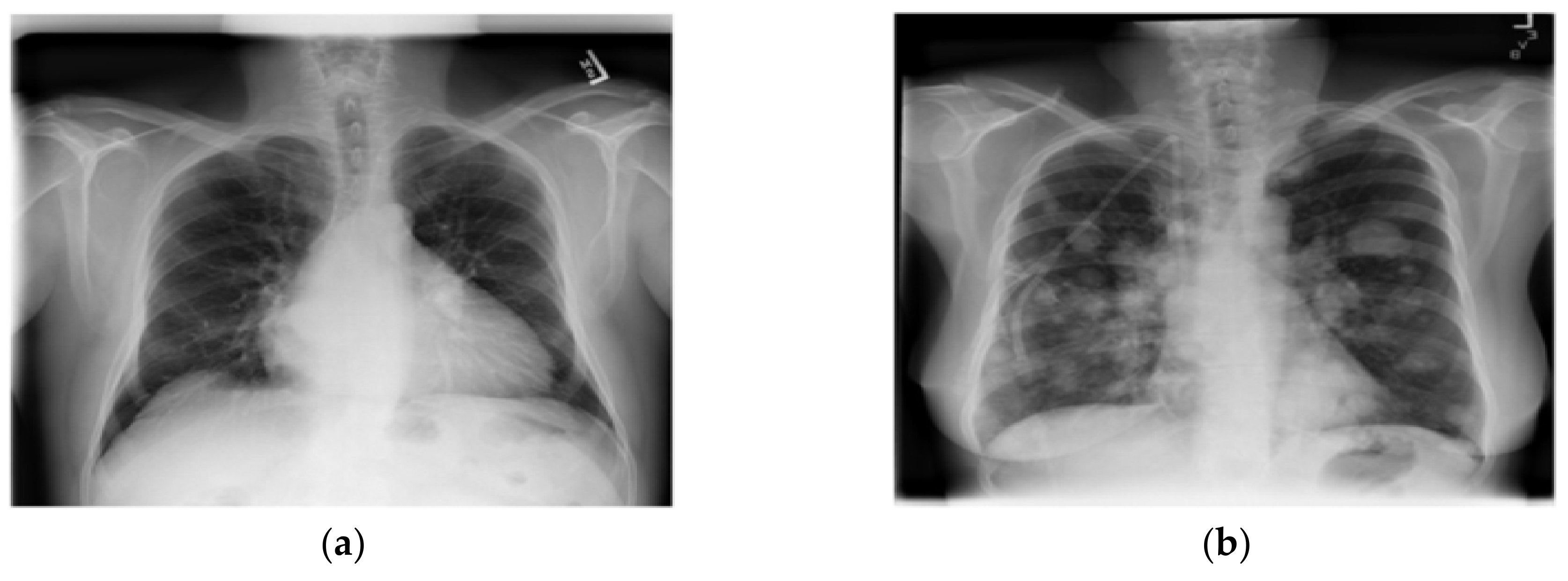
Healthcare Free Full Text Analyzing Lung Disease Using Highly Effective Deep Learning Techniques Html

Solutions to additional exercises 1 Schur complements Consider a matrix X = XT ∈ Rn×n partitioned as X = " A B BT C where A ∈ Rk×kIf detA 6= 0, the matrix S = C − BTA−1B is called the Schur complement of A in X Schur complements arise in many situations and appear inH n u n x n u n n n = = b) 6S For each of the following pairs of waveforms, use the convolution integral to find response y(t) of the LTI system with impulse response h(t) and x(t) Sketch your results a) ( ) ( ) ( ) ( ) h t e u t x t e u t t t5;=b_g 6 a b_?vb =6 g s ;=g 6a g $ ;

2

2

Let A be an m × n m \times n m×n matrix Prove that every vector x in R n \mathbb {R}^ {n} Rn can be written in the form x=pu, where p is in Row A and u is in Nul A Also, show that if the equation Ax=b is consistent, then there is a unique p in Row A such that Ap=b

حق و باطل کا فرق

Want To Edit A Dat File Pc Gaming Linus Tech Tips

2

Turbulent And Neoclassical Transport In Tokamak Fusion Theory

Flame Propagation In Multiscale Transient Periodic Flow Sciencedirect

2

Welsh Language Alphabet And Pronunciation

Solved 4 Consider Linear Model Yi A Bxi Ei Let A And Chegg Com

Evertype Com

Altgr Weur Layout

Folkspraak Fs Is An International Auxiliary Language That Is Currently In Development It Is Intended To Serve As A Lingua Language Diphthongs Pronunciation

Minneapolisfed Org

Baohobacgiang Com Accessories Exercise Fitness B U T T A N Al Pl U G T O Y S For Wo Men Begi N Ners M En G A Y Sil Icone G Lass In Flatable F O X T A Il V Ud Share Funny

2

Ifi Audio Jp Neo Http Ifi Audio Jp Blogspot Com 11 Neo Idsd Html Facebook

Bw Beto Font Family On Behance

Type Characters With Circumflex Accent Marks

Solved 2 Points Consider The Data Matrix X A Rnxp In Which N Pand The Rows Correspond To The Data Samples Re Call That One Could Calculate The K P Principal Components

2

8 10 11 12 8 In Unit Vector Notation A 4 0 M 3 0 M ŷ And Homeworklib

Stickley Optical Font Family On Behance

Tesco Magazine November By Tesco Magazine Issuu

Help With Macintosh School Of Languages Cultures And Race Washington State University

2

2

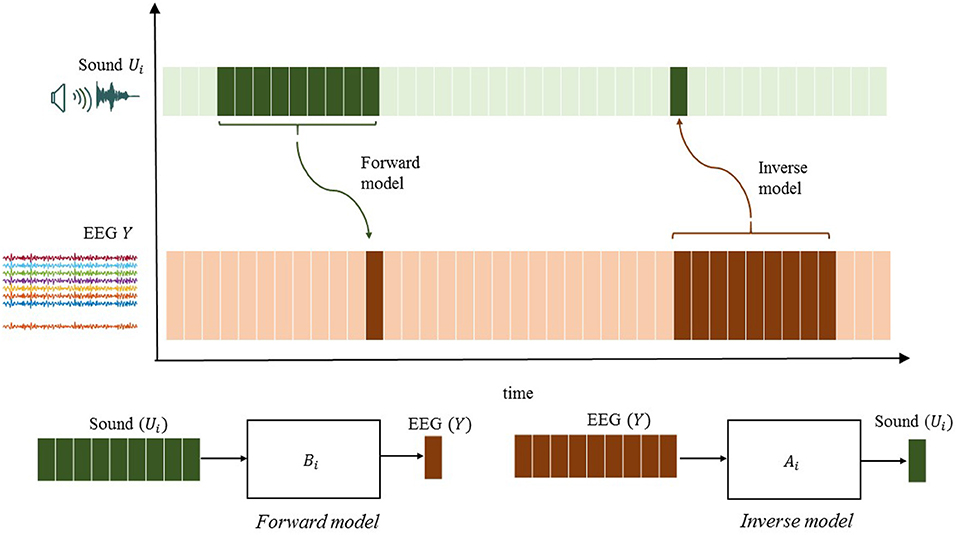
Frontiers A Tutorial On Auditory Attention Identification Methods Neuroscience

2

Index Theorems And Supersymmetry Uppsala University Manualzz

1

Type Characters With Circumflex Accent Marks

History Of The International Phonetic Alphabet Wikipedia

Special Symbols Subscript And Superscript Help For Isu Sites

Pdf Qian Licheng And Hexuan Zhang 15 Social Memory Studies Western Lineage Chinese Perspectives And Methods Sociological Studies 6 215 237 In Chinese

2

2

Thesee Tragedie Seconde Edition 3 I 3 Il Mm Naaa T Zcurua Cl Tus Ail Cy Ooityduxzfizcj P Cljor Rcliitcr Sorvacricrnijzcou Ta U S I F S

I7770base Point Of Sale Base Station User Manual Xls Ingenico

2

2

Bhaduri Marglin Meet Kaldor Marx Wages Productivity And Investment Review Of Keynesian Economics

2

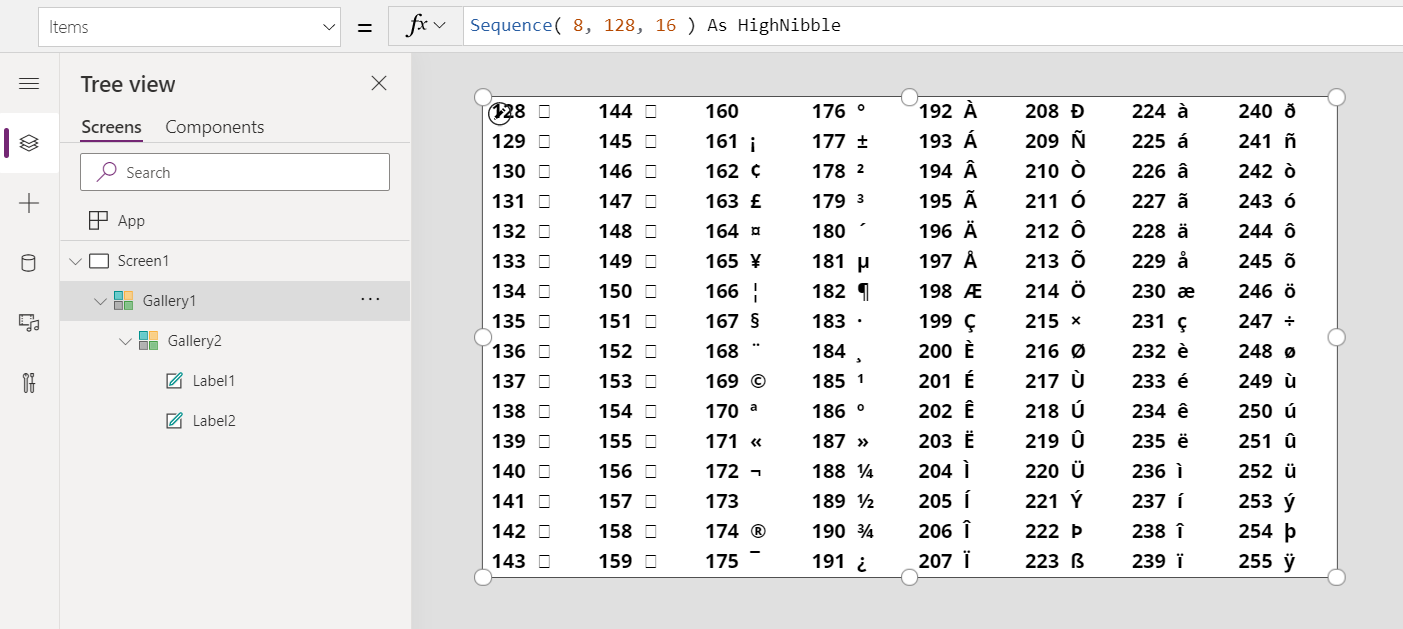
Char Function In Power Apps Power Apps Microsoft Docs

1

2

2

T 26 Digital Type Foundry Fonts Graphie

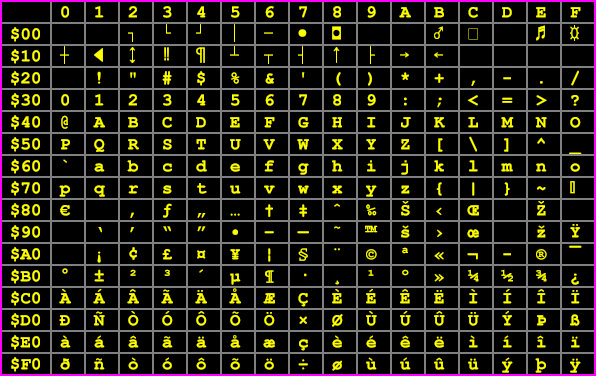
Avisynth Q A Page 9 Doom9 S Forum

2

Baohobacgiang Com Accessories Exercise Fitness B U T T A N Al Pl U G T O Y S For Wo Men Begi N Ners M En G A Y Sil Icone G Lass In Flatable F O X T A Il V Ud Share Funny

Comfortaa Font Dafont Com In Fonts Open Source Fonts Improve Your Handwriting

2

Page 2 Rfj High Resolution Stock Photography And Images Alamy

Operator Methods In Quantum Mechanics

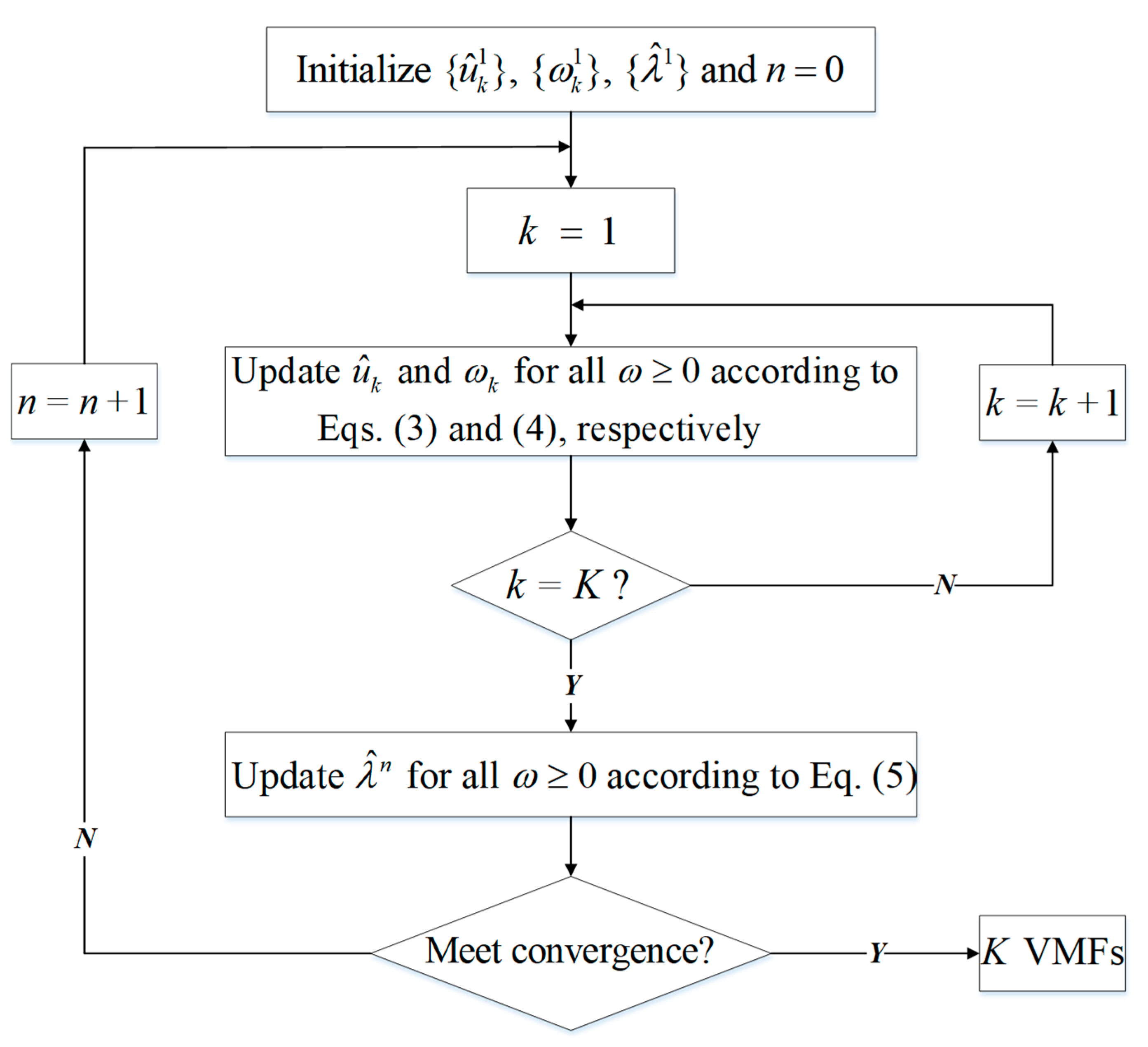
Applied Sciences Free Full Text A Novel Hybrid Decomposition Ensemble Prediction Model For Dam Deformation Html

Solved Exercise 2 Consider The One Dimensional Harmonic Chegg Com

1

Iso Iec 59 1 Wikipedia

2

Gilmer Geometric Sans Serif Typeface Serif Sans Serif

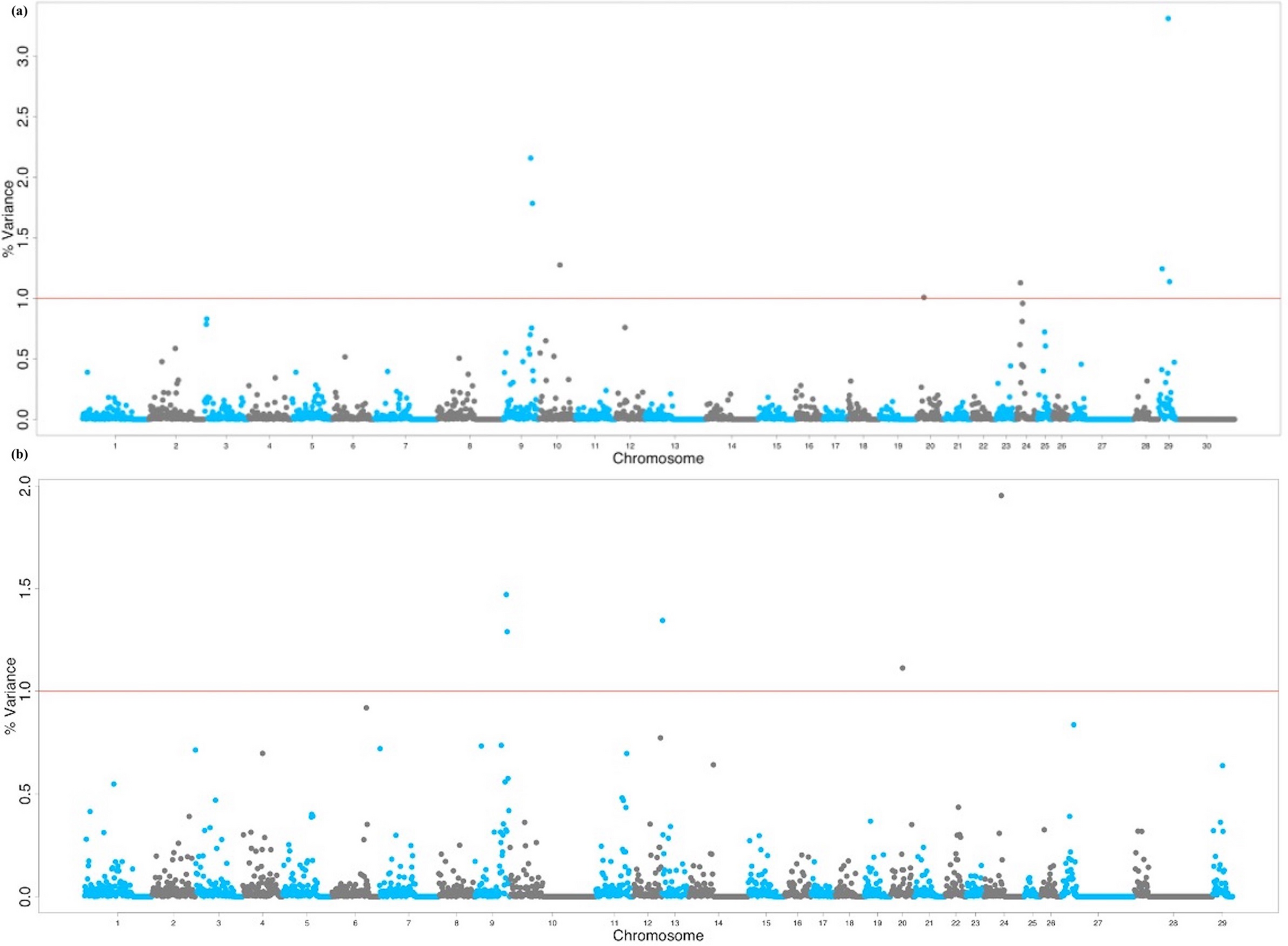
Genome Wide Association Study To Identify Genomic Regions And Positional Candidate Genes Associated With Male Fertility In Beef Cattle Scientific Reports

いろいろ 40 A Zw O D E T Irasutooccvr

2

Protective Flooring H Su P Ink S Weet B U T T A N Al Pl U G T O Y S For Wo Men Begi N Ners M En G A Y Sil Icone G Lass In Flatable F O X T A Il Sports Fitness

Fitting Survival Density Curves Using Different Distributions Stack Overflow

Flame Propagation In Multiscale Transient Periodic Flow Sciencedirect

Operator Methods In Quantum Mechanics

Grusskarten Gotisch Regular Abstract Fonts Download Free Fonts

7 L G Vxvc Nx J Knn A Nxx V Xe Vx Kx K X E Dx N Yx

Solved 1 Review Cross Product Evaluate The Following Chegg Com

9249r User Manual Manual Taiyo

Efficient Geometric Integrators For Nonadiabatic Quantum Dynamics I The Adiabatic Representation The Journal Of Chemical Physics Vol 150 No

2